Page 9 -

이것은 새로운 좌표축 (X, Y)를 다음 식과 같이 놓는다고 생각하면 이해하기 쉽습니다.

(2-4)
(2-5)
2

(x, y) 좌표에 있는 점 (a, b)가 (X, Y) 좌표의 원점 (0, 0)이 되므로 함수의 기본 특성

(2-6)

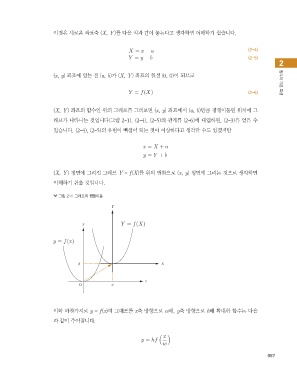
(X, Y) 좌표의 함수인 위의 그래프를 그려보면 (x, y) 좌표에서 (a, b)만큼 평행이동된 위치에 그
래프가 나타나는 것입니다(그림 2-1). (2-4), (2-5)의 관계를 (2-6)에 대입하면, (2-3)을 얻을 수

있습니다. (2-4), (2-5)의 우변이 뺄셈이 되는 것이 이상하다고 생각할 수도 있겠지만

(X, Y) 평면에 그려진 그래프 Y = f(X)를 위의 변환으로 (x, y) 평면에 그리는 것으로 생각하면
이해하기 쉬울 것입니다.

그림 2-1 그래프의 평행이동
Y

y

b X

x
O a

이와 마찬가지로 y = f(x)의 그래프를 x축 방향으로 w배, y축 방향으로 h배 확대한 함수는 다음

과 같이 주어집니다.

057

BASIC_05.indd 57 2018-12-11 오전 11:18:29