Page 23 -

그러면 증명을 시작하겠습니다. 우선 집합 S를 다음과 같이 정의합니다.

(2-25)
2
에 의해 S는 위로 유계인 집합이며, 1.3절의 정리 3 에 의해 다음과 같은 상한이 존
재합니다. 함수의 기본 특성

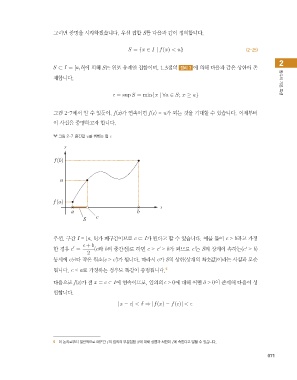
그림 2-7에서 알 수 있듯이, f(x)가 연속이면 f(c) = u가 되는 것을 기대할 수 있습니다. 이제부터
이 사실을 증명하고자 합니다.

그림 2-7 중간값 u를 취하는 점 c
y

u

x
a b
S c

우선, 구간 I = [a, b]가 폐구간이므로 c ∈ I가 된다고 할 수 있습니다. 예를 들어 c > b라고 가정
한 경우 (c와 b의 중간점)로 하면 c > c' > b가 되므로 c'는 S의 상계에 속하는(c' > b)

동시에 c보다 작은 원소(c > c')가 됩니다. 따라서 c가 S의 상한(상계의 최솟값)이라는 사실과 모순
됩니다. c < a로 가정하는 경우도 똑같이 증명됩니다. 5

다음으로 f(x)가 점 에 연속이므로, 임의의 > 0에 대해 어떤 δ > 0이 존재해 다음이 성
립합니다.

5 이 논리로부터 일반적으로 폐구간 I의 임의의 부분집합 S에 대해 상한과 하한이 I에 속한다고 말할 수 있습니다.

071

BASIC_05.indd 71 2018-12-11 오전 11:18:33