Page 14 -

ACT+
06 직각삼각형의 합동 조건 활용 스피드 정답 : 01쪽
친절한 풀이 : 12쪽

* 다음 그림과 같은 직각삼각형 ABC에서 Rx의 크기를
유형 1 RHS 합동의 활용
구하시오.

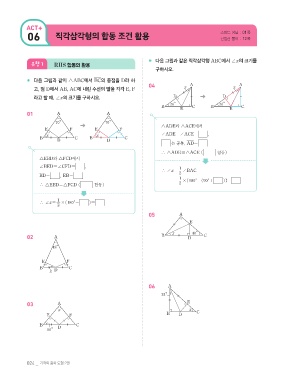
* 다음 그림과 같이 semoABC에서 5BC4의 중점을 D라 하
04 x A x A
고, 점 D에서 5AB4, 5AC4에 내린 수선의 발을 각각 E, F
라고 할 때, Rx의 크기를 구하시오. D D
36 æ 36 æ
B E C B E C
01 A A
70 æ 70 æ
semoADE와 semoACE에서
E F E F
x x RADE=RACE= 90° ,
B D C B D C
5AE4 는 공통, 5AD4= 5AC4
j semoADErsemoACE ( RHS 합동)
semoEBD와 semoFCD에서

RBED=RCFD= 90° ,
j Rx =1/2&RBAC
5BD4= 5CD4 , 5EB4= 5FC4
=1/2\{180°-(90°+ 36° )}= 27°
j semoEBDrsemoFCD ( RHS 합동)

j Rx=1/2\(180°- 70° )= 55°

05 A
E

x 40 æ C
02 A B D 25°
semoABErsemoDBE (RHS 합동)이므로
48 æ
Rx=1/2&RABD=1/2\{180°-(90°+40°)}=25°
E F
B C
x D 24°
semoEBDrsemoFCD (RHS 합동)이므로
RB=1/2\(180°-48°)=66° A
06
j Rx=180°-(90°+66°)=24°
24 æ
03 A E
x x C
E F B D 42°
semoABDrsemoAED (RHS 합동)이므로
B D C
50 æ 80° RDAE=RDAB=24°
j RBAC=24°+24°=48°
semoEBDrsemoFCD (RHS 합동)이므로 j Rx=180°-(90°+48°)=42°
RC=RB=50°
j Rx=180°-2\50°=80°

024 _ 기적의 중학 도형 2권

(011~040)중2도형1단원ok.indd 24 19. 7. 11. 오후 4:46