Page 10 -

ACT+
03 이등변삼각형의 성질 활용 스피드 정답 : 01쪽
친절한 풀이 : 10쪽

유형 1 겹쳐진 2개의 삼각형 유형 2 이웃한 이등변삼각형

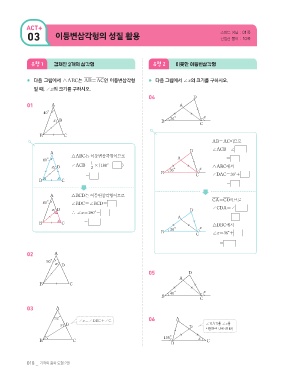
* 다음 그림에서 semoABC는 5AB4=5AC4인 이등변삼각형 * 다음 그림에서 Rx의 크기를 구하시오.
일 때, Rx의 크기를 구하시오.
04 D
01 A A
40 æ
x D B 36 æ x
C

B C
5AB4=5AC4이므로

A D RACB=R ABC
40 æ semoABC는 이등변삼각형이므로 A = 36°

x D RACB=1/2\(180°- 40° ) x semoABC에서
B 36 æ
= 70° C RDAC=36°+ 36°
B C
= 72°

A semoBCD는 이등변삼각형이므로
40 æ 5CA4=5CD4이므로
RBDC=RBCD= 70°
x D D RCDA=R CAD
j Rx =180°- 70°
A = 72°
B C = 110° semoDBC에서
36 æ x
B C Rx=36°+ 72°

= 108°
02 A
50 æ
x D
05 D
A 80 æ
B C 115° 80 æ

RC=1/2\(180°-50°)=65° 40 æ 40 æ x
B
RBDC=RBCD=65° j Rx=180°-65°=115° C 120°
03 A Rx=40°+80°=120°

52 æ 06 A
Rx=RDBC+RC 2x
x D 2x D RBAD를 Rx를
이용하여 나타내 봐!
105 æ x x
B C 96° C
B 35°
RB=1/2\(180°-52°)=64°
Rx+2Rx=105°
3Rx=105° j Rx=35°
RABD=1/2\64°=32°이므로 Rx=180°-(52°+32°)=96°
018 _ 기적의 중학 도형 2권

(011~040)중2도형1단원ok.indd 18 19. 7. 11. 오후 4:46