Page 8 -

ACT
02 이등변삼각형 설명 문제

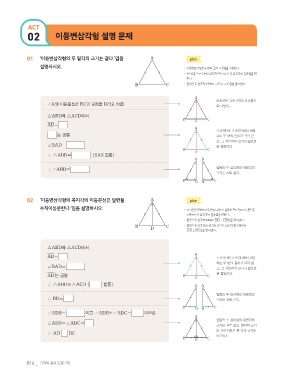
01 ‘이등변삼각형의 두 밑각의 크기는 같다.’임을 A plan
설명하시오. ㆍ 이등변삼각형은 두 변의 길이가 같음을 이용한다.
ㆍ 보조선을 그어 2개의 삼각형으로 나누고, 두 삼각형이 합동임을 밝
힌다.
B C ㆍ 합동인 두 삼각형으로부터 RB=RC임을 알아낸다.

A
보조선을 그어 2개의 삼각형으
∠A의 이등분선과 5BC4의 교점을 D라고 하면 로 나눈다.
semoABD와 semoACD에서
B C
D
5AB4= 5AC4
A
semoABD와 semoACD에서 대응
5AD4 는 공통 하는 두 변의 길이가 각각 같
고, 그 끼인각의 크기가 같으므
RBAD= RCAD 로 합동이다.
B C
D
j semoABDr semoACD (SAS 합동)
A A
합동인 두 삼각형의 대응각의
∴ ∠ABD= RACD
크기는 서로 같다.
B C
D D

02 ‘이등변삼각형의 꼭지각의 이등분선은 밑변을 A plan
수직이등분한다.’임을 설명하시오. ㆍ 이등변삼각형에서 두 변의 길이가 같음과 꼭지각의 이등분선을
이용하여 두 삼각형이 합동임을 밝힌다.
ㆍ 합동인 두 삼각형으로부터 5BD4=5CD4임을 알아낸다.
B C ㆍ 합동인 두 삼각형과 평각의 크기가 180°임을 이용하여
D 5AD4Z5BC4임을 알아낸다.

semoABD와 semoACD에서
A
5AB4= 5AC4 semoABD와 semoACD에서 대응
하는 두 변의 길이가 각각 같
RBAD= RCAD 고, 그 끼인각의 크기가 같으므
로 합동이다.
5AD4 는 공통 B D C
j semoABDrsemoACD ( SAS 합동) A A
합동인 두 삼각형의 대응변의
j 5BD4= 5CD4 길이는 서로 같다.
B C
D D
RADB= RADC 이고 RADB+RADC= 180° 이므로
A
합동인 두 삼각형의 대응각의
RADB=RADC= 90°
크기는 서로 같고, 평각의 크기
는 180°이므로 한 각의 크기는
j 5AD4 Z 5BC4
B D C 90°이다.

016 _ 기적의 중학 도형 2권

(011~040)중2도형1단원ok.indd 16 19. 7. 11. 오후 4:46