Page 5 -

VISUAL IDEA
1 이등변삼각형과 직각삼각형 V 직각삼각형의 합동 조건

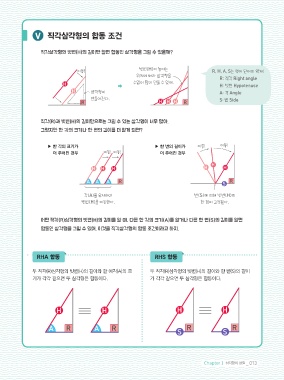
직각삼각형의 빗변(H)의 길이만 알면 합동인 삼각형을 그릴 수 있을까?

이동! 빗변(H)이 놓이는 R, H, A, S는 영어 단어의 약자!
V 이등변삼각형 “ 변의 길이, 각의 크기에 따라 삼각형 이름이 바뀌어!” 위치에 따라 삼각형을 R: 직각 Right angle
H H 수없이 많이 만들 수 있어. H: 빗변 Hypotenuse
H 삼각형이 H A: 각 Angle
만들어진다. R H H H H H H S: 변 Side
약속 두 변의 길이가 같은 삼각형을 이등변삼각형이라고 한다. R R R

二 等 邊 두 변의 길이가 같다는 뜻!
직각(R)과 빗변(H)의 길이만으로는 그릴 수 있는 삼각형이 너무 많아.
두 이 가장자리 변 그렇지만 한 각의 크기나 한 변의 길이를 더 알게 되면?
같을 등
▶한 각의 크기가 ▶한 변의 길이가 이동! 이동!
더 주어진 경우 이동! 이동! 더 주어진 경우

H H H H H H
성질 ➊ 이등변삼각형의 두 밑각의 크기는 서로 ➋ 이등변삼각형의 꼭지각의 이등분선은
같다. 밑변을 수직이등분한다.
A A A R S R

각(A)을 유지하며 변(S)에 의해 빗변(H)의
빗변(H)을 이동한다. 한 점이 고정된다.
크기가 수직이다.
같다.
어떤 직각(R)삼각형의 빗변(H)의 길이를 알 때, 다른 한 각의 크기(A)를 알거나 다른 한 변(S)의 길이를 알면
합동인 삼각형을 그릴 수 있어. 이것을 직각삼각형의 합동 조건이라고 하지.
이등분한다.

RHA 합동 RHS 합동
조건 이 조건을 만족하면 이등변삼각형이 된다. 이등변삼각형을 만드는 2가지 조건!
두 직각(R)삼각형의 빗변(H)의 길이와 한 예각(A)의 크 두 직각(R)삼각형의 빗변(H)의 길이와 한 변(S)의 길이
➊ 삼각형의 두 변의 길이가 같으면 이등변 ➋ 삼각형의 두 내각의 크기가 같으면 이등변 기가 각각 같으면 두 삼각형은 합동이다. 가 각각 같으면 두 삼각형은 합동이다.
삼각형이다. 약속에서 온 조건 삼각형이다. 성질에서 온 조건

H H H H

A R A R S R S R

012 _ 기적의 중학 도형 2권 ChapterⅠ 삼각형의 성질 _ 013

(011~040)중2도형1단원ok.indd 13 19. 7. 11. 오후 4:46