Page 15 -

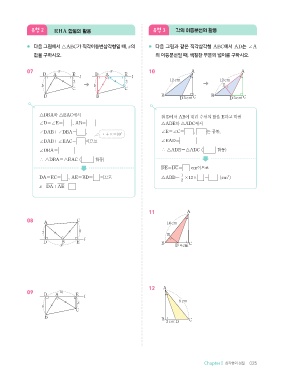
유형 2 RHA 합동의 활용 유형 3 각의 이등분선의 활용

* 다음 그림에서 semoABC가 직각이등변삼각형일 때, x의 * 다음 그림과 같은 직각삼각형 ABC에서 5AD4는 RA
값을 구하시오. 의 이등분선일 때, 색칠한 부분의 넓이를 구하시오.

07 D A x E D A x E 10 A A
l l
3 3 12`cm 12`cm
5 5 E
C C
B B B D 5`cm C B D 5`cm C

semoDBA와 semoEAC에서 점 D에서 5AB4에 내린 수선의 발을 E라고 하면
RD=RE= 90° , 5AB4= 5CA4 semoADE와 semoADC에서
RDAB+RDBA= 90° , RE=RC= 90° , 5AD4 는 공통,
•+\=90°
RDAB+REAC= 90° 이므로 READ= RCAD

RDBA= REAC j semoADErsemoADC ( RHA 합동)
j semoDBArsemoEAC ( RHA 합동)
5DE4=5DC4= 5 cm이므로
5DA4=5EC4= 3 , 5AE4=5BD4= 5 이므로 semoABD=1/2\12\ 5 = 30 (cm^2)

x=5DA4+5AE4= 8

11 A

08 A C 14`cm
7 8 E
l
D B E B
x 15 D 4`cm C 28 cm^2
semoADBrsemoBEC (RHA 합동)이므로 semoADErsemoADC (RHA 합동)이므로
x =5DB4+5BE4=5EC4+5AD4 5DE4=5DC4=4 cm
=8+7=15
j semoABD=1/2\14\4=28 (cm^2)

12 A
09 D A 10 E l

x 9`cm
6
C E
B 4 B C
semoDBArsemoEAC (RHA 합동)이므로 2`cm D 9 cm^2
semoABDrsemoAED (RHA 합동)이므로
x =5DA4=5DE4-5AE4=5DE4-5BD4
5DE4=5DB4=2 cm
=10-6=4
j semoADC=1/2\9\2=9 (cm^2)

Chapter I 삼각형의 성질 _ 025

(011~040)중2도형1단원ok.indd 25 19. 7. 11. 오후 4:46