Page 16 -

식에 사용된 e = 2.718…는 자연상수다. 이러한 형태의 분포를 푸아송분포

(Poisson distribution)라고 한다. 여기서 푸아송은 사람 이름이다.

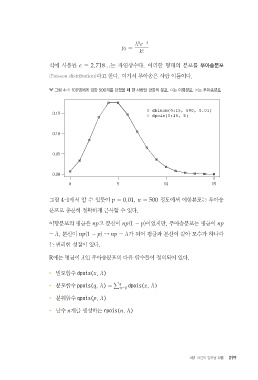
그림 4-1 100명에게 금화 500개를 던졌을 때 한 사람당 금화의 분포. ○는 이항분포, ×는 푸아송분포

dbinom(0:15, 500, 0.01)
0.15 dpois(0:15, 5)

0.10

0.05

0.00
0 5 10 15

그림 4-1에서 알 수 있듯이 p = 0.01, n = 500 정도에서 이항분포는 푸아송
분포로 충분히 정확하게 근사할 수 있다.

이항분포의 평균은 np고 분산이 np(1 − p)이었지만, 푸아송분포는 평균이 np
= λ, 분산이 np(1 − p) → np = λ가 되어 평균과 분산이 같아 모수가 하나라
는 편리한 성질이 있다.

R에는 평균이 λ인 푸아송분포의 다음 함수들이 정의되어 있다.

밀도함수 dpois(x, λ)
●
q
● 분포함수 ppois(q, λ) = ∑ =0 dpois(x, λ)
x
● 분위함수 qpois(p, λ)

● 난수 n개를 생성하는 rpois(n, λ)

4장 사건이 일어날 확률 099

0누구나통계 with R.indd 99 2018. 10. 26. 오전 12:29