Page 17 -

그런데 이 ‘부의 분포’에는 후일담이 있다.
신이 금화 5m개를 m명에게 평등하게 던지려고 했는데, 평균 5개인 것은 좋다 치고 분산도
5가 되어 버렸다. 빈부격차가 생기는 것을 원치 않던 신은 다음 방법으로 부를 재분배했다.
즉, 인간끼리 만나면 가위바위보를 해서 이긴 사람이 진 사람에게 금화 한 개를 받게 했다(단,
금화를 가지고 있지 않은 사람은 져도 금화를 주지 않는다). 가위바위보는 개인의 능력에 좌우
되지 않으므로 한 사람이 이길 확률과 질 확률은 같다. 이로써 빈부격차가 없어질 것이다.
하지만 실제로 해 보니 빈부격차가 오히려 더 커졌다. 한 사람당 평균 자산은 금화 5개로 그대
로고 가위바위보에 능력 차이가 없는데도 자유롭게 거래하면 그림 4-2의 오른쪽과 같이 지수
1
분포 가 되어 빈털터리가 되는 사람이 가장 많다는 결과가 나온다. 신은 가지지 못한 사람을
구제하기 위한 사회 보장 제도를 도입해야 한다.

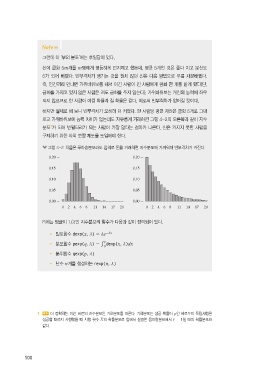
그림 4-2 처음은 푸아송분포라도 임의로 돈을 거래하면 지수분포에 가까워져 빈부격차가 커진다
0.20 0.20
0.15 0.15

0.10 0.10
0.05 0.05
0.00 0.00
0 2 4 6 8 11 14 17 20 0 2 4 6 8 11 14 17 20

R에는 평균이 1/λ인 지수분포의 함수가 다음과 같이 정의되어 있다.

● 밀도함수 dexp(x, λ) = λe −λx
q
● 분포함수 pexp(q, λ) = ∫ dexp(x, λ)dx
0
● 분위함수 qexp(p, λ)
● 난수 n개를 생성하는 rexp(n, λ)

1 역주 더 정확히는 이산 버전의 지수분포인 기하분포를 따른다. 기하분포는 성공 확률이 ρ인 베르누이 독립시행을
성공할 때까지 시행했을 때 시행 횟수 X의 확률분포로 앞에서 설명한 음이항분포에서 r = 1일 때의 확률분포와
같다.

100

0누구나통계 with R.indd 100 2018. 10. 26. 오전 12:29