Page 32 -

¯
̃
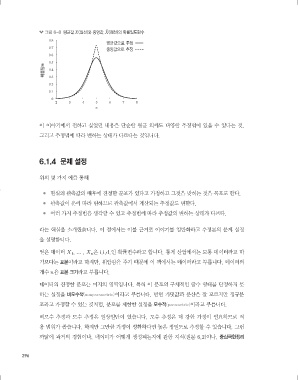
그림 6-8 평균값 X（실선)와 중앙값 X（점선)의 확률밀도함수
0.8
평균값으로 추정
0.7 중앙값으로 추정
0.6
0.5
확률밀도 0.4
0.3
0.2
0.1
0
2 3 4 5 6 7 8
x

이 이야기에서 전하고 싶었던 내용은 단순한 평균 외에도 다양한 추정법이 있을 수 있다는 것,
그리고 추정법에 따라 변하는 상태가 다르다는 것입니다.

6.1.4 문제 설정

위의 몇 가지 예를 통해

● 현실의 관측값의 배후에 진정한 분포가 있다고 가정하고 그것을 맞히는 것을 목표로 한다.
● 관측값이 운에 따라 변하므로 관측값에서 계산되는 추정값도 변한다.

● 여러 가지 추정법을 생각할 수 있고 추정법에 따라 추정값의 변하는 상태가 다르다.

라는 핵심을 소개했습니다. 이 절에서는 이를 근거로 이야기를 일반화하고 추정론의 문제 설정
을 설명합니다.

, 은 i.i.d.인 확률변수라고 합니다. 통계 산업에서는 보통 데이터라고 하
얻은 데이터 X 1 … , X n
기보다는 표본이라고 하지만, 위압감을 주기 때문에 이 책에서는 데이터라고 부릅니다. 데이터의
개수 n을 표본 크기라고 부릅니다.

데이터의 진정한 분포는 미지의 영역입니다. 특히 이 분포의 구체적인 함수 형태를 단정하지 못

하는 설정을 비모수적(nonparametric)이라고 부릅니다. 반면 기댓값과 분산은 잘 모르지만 정규분
포라고 가정할 수 있는 것처럼, 분포를 제한한 설정을 모수적（parametric）이라고 부릅니다.

비모수 추정과 모수 추정은 일장일단이 있습니다. 모수 추정은 더 강한 가정이 필요하므로 적
용 범위가 좁습니다. 하지만 그만큼 가정이 정확하다면 높은 정밀도로 추정할 수 있습니다. 그런
까닭에 과거의 경험이나, 데이터가 어떻게 생성되는지에 관한 지식（질문 6.2）이나, 중심극한정리

296

06 프로그래머를 위한 확률통계.indd 296 2019. 4. 25. 오전 11:41