Page 29 -

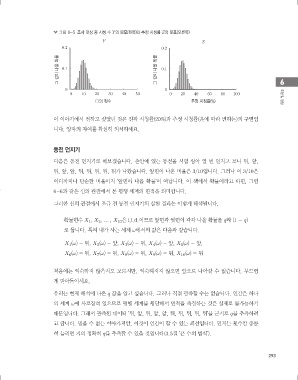
그림 6-5 조사 대상 중 시청 수 Y의 분포(왼쪽)와 추정 시청률 Z의 분포(오른쪽)
Y Z
0.2 0.2
그 값이 나올 확률 0.1 그 값이 나올 확률 0.1

0 0 6
0 10 20 30 40 50 0 20 40 60 80 100 추정 및 검정
◯의 횟수 추정 시청률(%)

이 이야기에서 전하고 싶었던 것은 진짜 시청률(20%)과 추정 시청률(운에 따라 변하는)의 구별입
니다. 양자의 차이를 확실히 의식하세요.

동전 던지기

다음은 동전 던지기로 해보겠습니다. 손안에 있는 동전을 시험 삼아 열 번 던지고 보니 뒤, 앞,
뒤, 앞, 앞, 뒤, 뒤, 뒤, 뒤, 뒤가 나왔습니다. 앞면이 나온 비율은 3/10입니다. 그러나 이 3/10은
어디까지나 단순한 비율이지 ‘앞면이 나올 확률’이 아닙니다. 이 책에서 확률이라고 하면, 그림
6-6과 같은 신의 관점에서 본 평행 세계의 면적을 의미합니다.

그러한 신의 관점에서 조금 전 동전 던지기의 실험 결과는 이렇게 해석됩니다.

,
확률변수 X 1 , X 2 … , X 10 은 i.i.d.이므로 앞면과 뒷면이 각각 나올 확률을 q와 (1 2 q)
로 둡니다. 특히 내가 사는 세계 ω에서의 값은 다음과 같습니다.

X 1 (ω) 5 뒤, X 2 (ω) 5 앞, X 3 (ω) 5 뒤, X 4 (ω) 5 앞, X 5 (ω) 5 앞,

X 6 (ω) 5 뒤, X 7 (ω) 5 뒤, X 8 (ω) 5 뒤, X 9 (ω) 5 뒤, X 10 (ω) 5 뒤

처음에는 익숙하지 않을지도 모르지만, 익숙해지지 않으면 앞으로 나아갈 수 없습니다. 부드럽
게 받아들이세요.

우리는 현재 해석에 나온 q 값을 알고 싶습니다. 그러나 직접 관측할 수는 없습니다. 인간은 하나

의 세계 ω에 사로잡혀 있으므로 평행 세계를 횡단해서 면적을 측정하는 것은 실제로 불가능하기
때문입니다. 그래서 관측된 데이터 ‘뒤, 앞, 뒤, 앞, 앞, 뒤, 뒤, 뒤, 뒤, 뒤’를 근거로 q를 추측하려
고 합니다. 믿을 수 없는 이야기지만, 이것이 인간이 할 수 있는 최선입니다. 던지는 횟수만 충분
히 늘리면 거의 정확히 q를 추측할 수 있을 것입니다（3.5절 ‘큰 수의 법칙’).

293

06 프로그래머를 위한 확률통계.indd 293 2019. 4. 25. 오전 11:41