Page 5 -

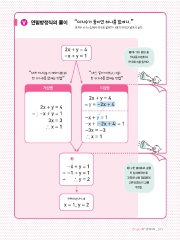
VISUAL IDEA “ 미지수가 둘이면 하나를 없애자.”
1 연립방정식 V 연립방정식의 풀이 미지수 x나 y 중에서 하나를 없애고 나머지 하나만 남겨서 푼다.

V 여러 가지 일차방정식 2x + y = 4 ❶ 두 가지 방법 중
−x + y = 1 하나를 이용하여

한 미지수를 없앤다.
▶ 미지수가 1개인 ▶ 미지수가 2개인 ▶ 미지수가 2개인
일차방정식 일차방정식 연립일차방정식
“ 더하거나(加,가) 빼서(減,감) “ 대신 넣어서(代入,대입)
한 미지수를 없애는 방법 ” 한 미지수를 없애는 방법 ”

미지수 미지수
미지수 미지수 미지수 가감법 대입법
ax + b = 0 ax + by + c = 0 ax + by + c = 0
dx + ey + f = 0 2x + y = 4

y = −2x + 4
2x + y = 4
미지수가 1개이고, 미지수가 2개이고, 미지수가 2개인 두 일차방정
그 차수가 1인 방정식 그 차수가 1인 방정식 식을 한 쌍으로 묶어 놓은 것 − −x + y = 1
(단, a, b는 상수, a≠0) (단, a, b, c는 상수, a, b≠0) (단, a, b, c, d, e, f는 상수, −x + y = 1
a, b, d, e≠0) 3x = 3 −x + (−2x + 4) = 1
x = 1
2x = 4 2x + y = 4 2x + y = 4 −3x = −3

−x + y = 1 x = 1

해를 구하면? 해를 구하면? 해를 구하면?

x 1 2 3 … x 1 2 3 … x 1 2 3 … 1

y 2 0 −2 … y 2 0 −2 … −x + y = 1
x = 2 x = 1, y = 2 x 1 2 3 … −1 + y = 1 ❷ 구한 미지수의 값을
두 일차방정식 중
x = 2, y = 0 y 2 3 4 … y = 2 간단한 식에 대입하여

x = 3, y = −2 다른 미지수의 값을
x = 1, y = 2 구한다.

…
연립방정식의 해
“ 해의 수는 딱 1개! “ 해의 수는 여러 개! “ 해의 수는 보통 1개! x = 1, y = 2
”
”
해의 꼴은 x = ? ” 해의 꼴은 x=?, y=? 해의 꼴은 x=?, y=?

012 _ 기적의 중학 연산 2B ChapterⅣ 연립방정식 _ 013

기적의중학연산_2B-4_본문_육.indd 13 2018-12-05 오후 2:02:12