Page 5 -

약속·성질·공식만
잘 기억하면
문제 풀이가 술술~

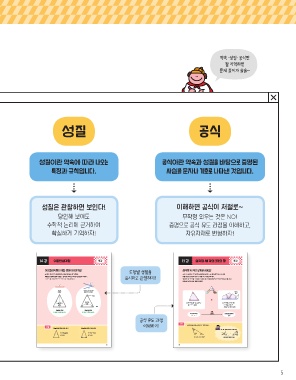
성질 공식

성질이란 약속에 따라 나오는 공식이란 약속과 성질을 바탕으로 증명된
특징과 규칙입니다. 사실을 문자나 기호로 나타낸 것입니다.

⇠ ⇠

성질은 관찰하면 보인다! 이해하면 공식이 저절로~
당연해 보여도 무작정 외우는 것은 NO!
수학적 논리에 근거하여 증명으로 공식 유도 과정을 이해하고,

확실하게 기억하자! 자유자재로 변형하자!

14 강 이등변삼각형 13 강 삼각형 세 각의 크기의 합
이등변삼각형은 어떤 성질이 있을까요? 도형별 성질을 삼각형 세 각의 크기를 더하면?
두 변의 길이가 같은 삼각형을 이등변삼각형이라고 약속했어요. 크기가 큰 삼각형, 작은 삼각형, 뒤집어진 삼각형 등 크기와 모양은 서로 다르지만
이등변삼각형에서 길이가 같은 두 변이 만나도록 반으로 접으면 완전히 포개져요. 표시하고 관찰하기! 어떤 모양의 삼각형도 세 각의 크기를 모두 더하면 180°예요.
그러므로 이등변삼각형은 두 각의 크기도 항상 같답니다. 왜냐하면 삼각형의 세 꼭짓점을 한 점에 모이도록 이어 붙이면 일직선이 만들어지기 때문이죠.
일직선이 180°인 사실, 까먹지 않았죠?
접으면 크기가 같은 두 각은 밑각,
포개져요. 나머지 한 각은 꼭지각 일직선은
180°
꼭지각
크기가
길이가 같다. ➊ 삼각형의 세 각을 표시한 후 ➋ 삼각형의 세 꼭짓점이
같다. 세 조각으로 잘라요. 한 점에서 모이도록
밑각 겹치지 않게 이어 붙여요.
이등변삼각형은 이등변삼각형은
두 변의 길이가 같습니다. 두 각의 크기가 같습니다.
세 각이 모여서 일직선을 만들어요.
+ + 180°
공식 유도 과정
이해하기! 공식 삼각형의 세 각의 크기의 합은 180°입니다.
성질
이등변삼각형 변의 성질 이등변삼각형 각의 성질
ﾡ 세 각의 크기의 합이 180°가 아니라면?
두 변의 길이가 두 각의 크기가 ﾤ 55 ̊ → 55 ̊
같습니다. 같습니다. ﾧ 45 ̊ 90 ̊ 45 ̊ 90 ̊
㉠ + ㉡ + ㉢ = 180° 삼각형이 만들어지지 않아요.
63 58
5

기적특강(도형편)1권001-052.indd 5 23. 12. 6. 오후 1:46