Page 17 -

* 맞은 개수 *

스피드 정답 : 04쪽
친절한 풀이 : 17쪽 15

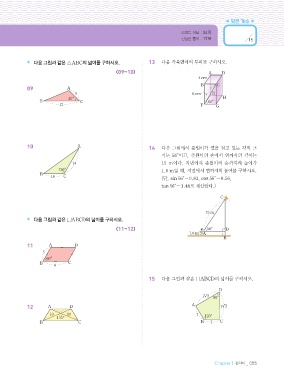
* 다음 그림과 같은 semoABC의 넓이를 구하시오. 13 다음 직육면체의 부피를 구하시오.

(09~10) A D
4`cm
B C
09 A
5 6`cm E
45æ H
B C 60æ
12 15rt2 F G 36rt3 cm^3
semoABC=1/2\12\5\sin 45° ^-FG^-=6 cos 60°=6\1/2=3 (cm)
rt2
=1/2\12\5\ =15rt2 rt3
2 ^-CG^-=6 sin 60°=6\ =3rt3 (cm)
2
∴ (직육면체의 부피)
=3\3rt3\4=36rt3 (cm^3)
10 A 14 다음 그림에서 준원이가 연을 잡고 있는 각의 크
기는 56°이고, 준원이의 손에서 연까지의 길이는
14 15 m이다. 지면에서 준원이의 손까지의 높이가
120æ 1.6 m일 때, 지면에서 연까지의 높이를 구하시오.
B
10 C 35rt3 (단, sin 56°=0.83, cos 56°=0.56,
semoABC=1/2\10\14\sin (180°-120°)
tan 56°=1.48로 계산한다.)
rt3
=1/2\10\14\ =35rt3
2 C

15`m
* 다음 그림과 같은 nemoABCD의 넓이를 구하시오.

(11~12) 56æ D
1.6`m A
B 14.05 m
11 " % ^-BD^-=(지면에서 준원이의 손까지의 높이)=1.6 m
semoACD에서
^-CD^-=15 sin 56°=15\0.83=12.45 (m)
60æ
# $ ∴ (지면에서 연까지의 높이)
20rt3 =^-CD^-+^-DB^-=12.45+1.6=14.05 (m)
nemoABCD=8\5\sin 60°
rt3
=8\5\ =20rt3 15 다음 그림과 같은 nemoABCD의 넓이를 구하시오.
2
D
7Â3 60æ

12 " % A 7Â3
10 10 7
135æ 120æ
# $ 25rt2 B 7 C 49rt3
nemoABCD=1/2\10\10\sin (180°-135°) rt3 49rt3
semoABC=1/2\7\7\sin (180°-120°)=1/2\7\7\ =
2 4
rt2
=1/2\10\10\ =25rt2 rt3 147rt3
2 semoACD=1/2\7rt3\7rt3\sin 60°=1/2\7rt3\7rt3\ =
2 4
49rt3 147rt3
∴ nemoABCD =semoABC+semoACD= + =49rt3
4 4
Chapter I 삼각비 _ 055

중3도형-본문(011~056)1단원.indd 55 20. 4. 28. 오후 2:55