Page 5 -

VISUAL IDEA
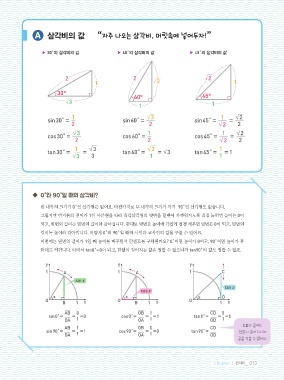
1 삼각비 A 삼각비의 값 “ 자주 나오는 삼각비, 머릿속에 넣어두자!”

▶ 30˚의 삼각비의 값 ▶ 60˚의 삼각비의 값 ▶ 45˚의 삼각비의 값

V 삼각비의 정의 2 2 2 11 1 2 2 2 3 3 3 2 2 2 1 1 1

30°
30°30°
45°
60°
60°
직각삼각형에서 각의 크기는 그대로 둔 채 변의 길이만 늘리면 60° 45° 45°
세 변의 길이 사이의 비는 어떻게 달라질까? 3 3 3 1 1 1
1 1 1
만들어진 삼각형들을 잘 살펴봐. 모두 닮은 도형이지! 1 3 1 2
이때 세 변의 길이의 비(닮음비)는 항상 같아. sin 30˚= sin 60˚= sin 45˚= =
2 2 2 2
이때 두 변의 길이의 비를 c 3 cos 30˚= 3 cos 60˚= 1 cos 45˚= 1 = 2
삼각비라고 부르자. 2 2 2 2
c 2 a 3 …
1
a tan 30˚= 1 = 3 tan 60˚= 3 = 3 tan 45˚= = 1
c 1 2 3 3 1 1
a
a 1 = = = … a 1
a
3
2
c 1 c 2 c 3
b
b
b 1 = = = …
3
2
c 1 c 2 c 3 α
a
a 1 = = = … b 1 ≂ 0 와 90 일 때의 삼각비?
a
°
°
3
2
b 1 b 2 b 3 b 2 b 3 한 내각의 크기가 0˚인 삼각형은 없어요. 마찬가지로 두 내각의 크기가 각각 90˚인 삼각형도 없습니다.
그렇지만 반지름의 길이가 1인 사분원을 따라 직각삼각형의 빗변을 밑변에 가까워지도록 점점 눕히면 높이는 0이
“ 직각삼각형에서 각의 크기가 정해지면 되고, 빗변의 길이는 밑변의 길이와 같아집니다. 반대로 빗변을 높이에 가깝게 점점 세우면 밑변은 0이 되고, 빗변의
길이는 높이와 같아집니다. 이렇게 0˚와 90˚일 때의 사인과 코사인의 값을 구할 수 있어요.
삼각형의 크기와 상관없이 변의 길이의 비가 일정하다.” 이번에는 밑변의 길이가 1일 때 높이를 바꾸면서 탄젠트를 구해볼까요? 0˚이면 높이가 0이고, 90˚이면 높이가 무
한대로 커집니다. 따라서 tan0˚= 0이 되고, 한없이 길어지는 값은 정할 수 없으니까 tan90˚의 값도 정할 수 없죠.
∠α의 사인 ∠α의 코사인 ∠α의 탄젠트 y y y

1 A 1 A 1 C
sinx
tanx
c a c a x x cosx x D

α α α O B 1 x O B 1 x O 1 x
b b AB 0 OB 1 CD 0
sin 0˚= OA = =0 cos 0˚= OA = =1 tan 0˚= OD = =0
1
1
1
sin α= 높이 = a cos α= 밑변 = b tan α= 높이 = a sin 90˚= AB = =1 cos 90˚= OB = =0 tan 90˚= CD CD의 길이는
1
0
한없이 길어지니까
빗변 c 빗변 c 밑변 b OA 1 OA 1 OD 값을 정할 수 없어요.

012 _ 기적의 중학 도형 3권 ChapterⅠ 삼각비 _ 013

중3도형-본문(011~056)1단원.indd 13 20. 4. 28. 오후 2:55