Page 4 -

VISUAL IDEA
1 이차방정식 A 이차방정식의 풀이법

▶ 인수분해 이용하기

2
x +7x+10=0 (완전제곱식)=0 꼴로 인수분해되면?
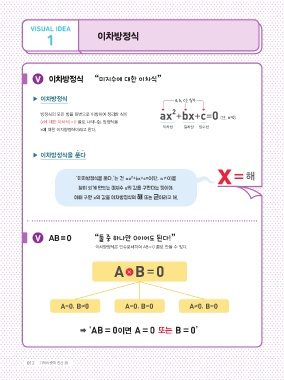
V 이차방정식 “ 미지수에 대한 이차식” 인수분해 답이 하나, 즉 중근!

합이 +7, 곱이 +10이
되는 두 수 : +2, +5 2
▶ 이차방정식 a, b, c는 실수 (x+2)(x+5)=0 x +6x+9=0
인수분해
2 A B AB=0이면 a +2ab+b 2
2
방정식의 모든 항을 좌변으로 이항하여 정리한 식이 =(a+b) 2
ax +bx+c=0 (단, a≠0) A=0 또는 B=0
(x에 대한 이차식)＝0 꼴로 나타나는 방정식을 (x+3) =0
2
또는
이차항 일차항 상수항 x+2=0 x+5=0
x에 대한 이차방정식이라고 한다.
식이 하나뿐이므로
x+3=0
∴ x=-2 x=-5 ∴ x=-3
또는
▶ 이차방정식을 푼다
x x ==

2
‘이차방정식을 푼다.’는 건 ax +bx+c=0(단, a≠0)을 해해
참이 되게 만드는 미지수 x의 값을 구한다는 뜻이야.
제곱근을 이용한다면? ▶ 완전제곱식과 제곱근 활용하기
이때 구한 x의 값을 이차방정식의 해 또는 근이라고 해.
±루트로 나타내기! x에 대한 부분을 먼저 완전제곱식으로 만들고, 제곱근의

정의(■ = a →■=± a)를 이용하여 해를 구한다.
2
2
4(x-5) =8
2
x +4x-6=0
V AB＝0 “ 둘 중 하나만 0이어도 된다!” 2 상수항을 우변으로
2
이차방정식은 인수분해하여 AB＝0 꼴로 만들 수 있다. (x-5) =2 x +4x =6
2
(x+p) =q (q≥0) 양변에
x+p=± q { (일차항의 계수) 2 더하기
2 }
=
A B 0 x-5=± 2 x +4x+4=6+4
2
×
완전제곱식 만들기
2
∴ x=5± 2 (x+2) =10
제곱근을 이용하기
,
,
,
A=0 B≠0 A=0 B=0 A≠0 B=0 x+2=± 10

‘AB＝0이면 A＝0 또는 B＝0’ ∴ x=-2± 10

012 _ 기적의 중학 연산 3B ChapterⅤ 이차방정식 _ 013

(011~054)중3B연산5단원ok.indd 12 19. 12. 6. 오후 3:46