Page 20 -

결과
[36 22 28 23 25 18 30 27 34 26 33 31 26 26 32 26 23 32 2
33 33 27 26 35 20 32 44 23 30 26 9 11 9 6 8 7 1
8 5 6 5 9 5 7 6 5 11 5 5 10 9 4 5 7 5
9 8 10 5 7 9 5 6 3 8 7 4 6 7 7 4 5 3 PyMC 더 알아보기
5 6 8 10 5 6 8 5]

5. 가상의 데이터셋을 그린다.

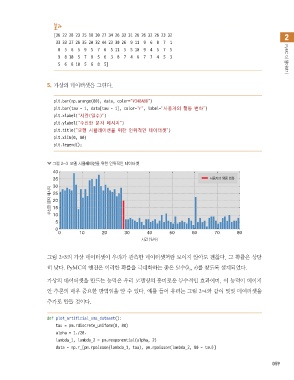
plt.bar(np.arange(80), data, color=”#348ABD”)
plt.bar(tau - 1, data[tau - 1], color=”r”, label=”사용자의 행동 변화")
plt.xlabel(“시간(일수)”)
plt.ylabel(“수신한 문자 메시지")
plt.title(“모델 시뮬레이션을 위한 인위적인 데이터셋”)
plt.xlim(0, 80)
plt.legend();

그림 2-3 모델 시뮬레이션을 위한 인위적인 데이터셋
40
35 ࢎਊ੗੄ ೯ز ߸ച
30
ࣻनೠ ޙ੗ ݫद૑ 25
20
15
10
5
0
0 10 20 30 40 50 60 70 80
दр ੌࣻ

그림 2-3의 가상 데이터셋이 우리가 관측한 데이터셋처럼 보이지 않아도 괜찮다. 그 확률은 상당
히 낮다. PyMC의 엔진은 이러한 확률을 극대화하는 좋은 모수(λ, τ)를 찾도록 설계되었다.
i
가상의 데이터셋을 만드는 능력은 우리 모델링의 흥미로운 부수적인 효과이며, 이 능력이 베이지
안 추론의 매우 중요한 방법임을 알 수 있다. 예를 들어 우리는 그림 2-4와 같이 몇몇 데이터셋을

추가로 만들 것이다.

def plot_artificial_sms_dataset():
tau = pm.rdiscrete_uniform(0, 80)
alpha = 1./20.
lambda_1, lambda_2 = pm.rexponential(alpha, 2)
data = np.r_[pm.rpoisson(lambda_1, tau), pm.rpoisson(lambda_2, 80 - tau)]

059

베이지안_11.indd 59 2017-11-17 오전 11:07:25