Page 15 -

%matplotlib inline
from IPython.core.pylabtools import figsize
from matplotlib import pyplot as plt
figsize(12.5, 4)
plt.rcParams[‘savefig.dpi’] = 300
plt.rcParams[‘figure.dpi’] = 300
samples = [lambda_1.random() for i in range(20000)]
plt.hist(samples, bins=70, normed=True, histtype=”stepfilled”)
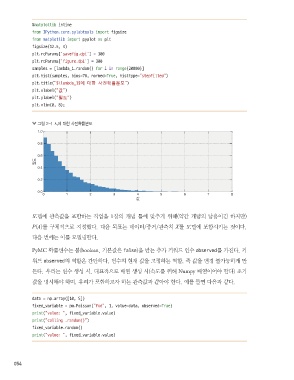
plt.title(“$\lambda_1$에 대한 사전확률분포”)
plt.xlabel(“값”)
plt.ylabel(“밀도”)
plt.xlim(0, 8);

그림 2-1 λ 1 에 대한 사전확률분포
1.0

0.8

0.6
޻ب
0.4

0.2
0.0
0 1 2 3 4 5 6 7 8
ч

모델에 관측값을 포함하는 작업을 1장의 개념 틀에 맞추기 위해(약간 개념의 남용이긴 하지만)

P(A)를 구체적으로 지정했다. 다음 목표는 데이터/증거/관측치 X를 모델에 포함시키는 것이다.
다음 번에는 이를 모델링한다.

PyMC 확률변수는 불(boolean, 기본값은 false)을 받는 추가 키워드 인수 observed를 가진다. 키
워드 observed의 역할은 간단하다. 변수의 현재 값을 고정하는 역할, 즉 값을 변경 불가능하게 만
든다. 우리는 변수 생성 시, 대표적으로 배열 생성 시(속도를 위해 Numpy 배열이어야 한다) 초기
값을 명시해야 하며, 우리가 포함하고자 하는 관측값과 같아야 한다. 예를 들면 다음과 같다.

data = np.array([10, 5])
fixed_variable = pm.Poisson(“fxd”, 1, value=data, observed=True)
print(“value: “, fixed_variable.value)
print(“calling .random()”)
fixed_variable.random()
print(“value: “, fixed_variable.value)

054

베이지안_11.indd 54 2017-11-17 오전 11:07:24