Page 26 -

베이즈 통계에서는 데이터를 얻은 후의 분포임을 강조해서 p(θ|Y )를 사후분포(posterior
distribution)라고 부른다. 문맥에 따라서는 사후확률(posterior probability)이라고 부르기도 한다. 반
대로 데이터를 얻기 전 분포 p(θ)를 사전분포(prior distribution)라 부른다. 마찬가지로 사전확률(prior

probability)이라 부르기도 한다. 사후분포는 베이즈 정리를 사용해서 다음과 같이 구할 수 있다.

즉, 사후분포 p(θ|Y)는 가능도 p(Y|θ)와 사전분포 p(θ)의 곱에 비례한다는 의미다. 여기서 p(Y)
는 이미 얻은 데이터 Y에만 의존하고 θ에는 의존하지 않는 상수 값이다. 다시 말해 p(Y|θ) p(θ)

가 θ 분포의 형태를 만들고 p(Y)는 그 형태를 정규화하는 정규화 상수로 볼 수 있다. 가능도와 사
전분포 계산은 간단하지만 p(Y) 계산은 일반적으로 간단하지 않다. 이런 상황에서 정규화 상수
인 p(Y)를 무시하고 사후분포에 비례하는 분포 p(Y|θ) p(θ)에서 난수 표본을 많이 생성시켜서

사후분포 대신 사용한다. 이 아이디어가 MCMC다. MCMC에서 얻은 난수 표본을 이 책에서는
MCMC 표본이라고 부른다. 사후분포 대신에 MCMC 표본을 사용해 여러 통계량의 계산이나 적
분 계산을 수행한다. MCMC 표본을 생성하는 알고리즘으로 메트로폴리스-헤이스팅스 알고리즘
(Metropolis-Hastings algorithm)이나 깁스 샘플링(Gibbs sampling)이 많이 알려져 있다. Stan에서는
1.4절에서 이야기한 대로 NUTS를 사용한다.

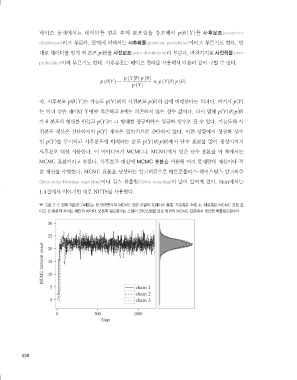
그림 2-2 왼쪽 꺾은선 그래프는 한 매개변수의 MCMC 표본 수열의 트레이스 플롯. 가로축은 스텝 수, 세로축은 MCMC 표본 값
이고 선 종류의 차이는 체인의 차이다. 오른쪽 밀도함수는 스텝이 200스텝을 넘은 범위의 MCMC 표본에서 계산한 확률밀도함수다

MCMC sample value

Step

038

1데이터분석을위한베이지안통계모델링.indd 38 2019. 3. 14. 오후 8:32